オイラーの公式

数学の複素解析におけるオイラーの公式（オイラーのこうしき、英: Euler's formula）とは、複素指数関数と三角関数の間に成り立つ、以下の恒等式のことである：

e^{iz}=\cos z i\sin z

ここで $z$ は任意の複素数、 $e$ はネイピア数、 $i$ は虚数単位、 $\cos$ は余弦関数、 $\sin$ は正弦関数である。

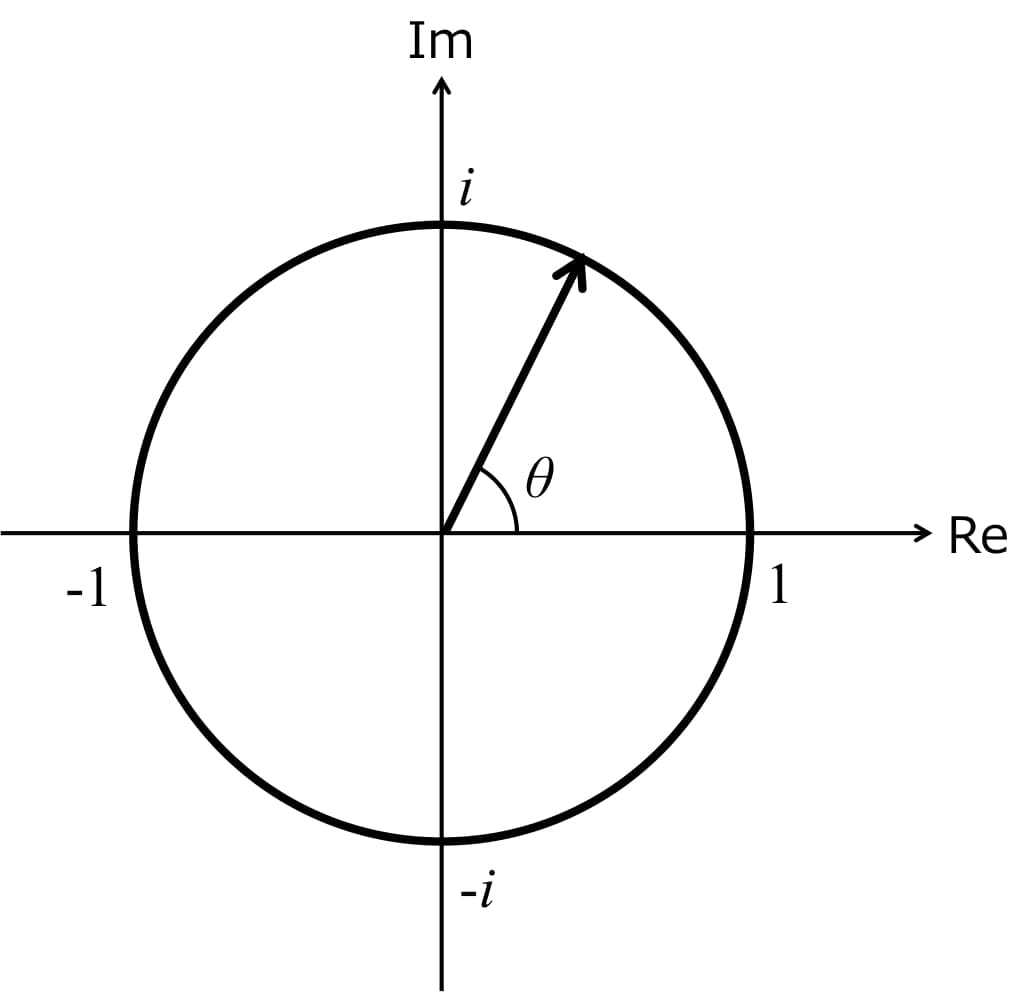
特に、 $z=\varphi (\in \mathbb {R} )$ とする場合がよく使われ、この場合、 $e^{i\varphi }$ は、絶対値 $1$ , 偏角 $\varphi [\mathrm {rad} ]$ の複素数に等しい。

オイラーの公式は、複素解析をはじめとする数学の様々な分野や、電気工学・物理学などで現れる微分方程式の解析において重要である。物理学者のリチャード・P・ファインマンはこの公式を評して「我々の至宝」かつ「すべての数学のなかでもっとも素晴らしい公式」 だと述べている。

概要

この公式の名前は、18世紀の数学者レオンハルト・オイラーに因むが、最初の発見者はロジャー・コーツとされる。コーツは1714年に

\log \left(\cos x i\sin x\right)=ix\

を発見したが、三角関数の周期性による対数関数の多価性を見逃した。1740年頃、オイラーは、コーツの公式を基に、指数関数と三角関数の級数展開を比較することによって、オイラーの公式を証明し、1748年に発表した。

オイラーの公式を導入することにより、極形式の複素数は、より簡素な表記に変換することができる。すなわち、複素数の極形式 z = r(cos θ i sin θ) は z = re^iθ に等しい。また、特に、θ = π のとき、

e^{i\pi } 1=0

が導かれる。この関係式はオイラーの等式 (Euler's identity) と呼ばれる。

オイラーの公式により、余弦関数および正弦関数は、双曲線関数に変換することができる：

\cos \theta =\cosh i\theta

\sin \theta ={\tfrac {1}{i}}\sinh i\theta

応用上では、三角関数を複素指数関数に置き換えることで、微分方程式やフーリエ級数などが利用しやすくなる。

指数関数と三角関数

実関数としての指数関数 e^x, 三角関数 cos x, sin x をそれぞれマクローリン展開すると

となる。これらの冪級数の収束半径が ∞ であることは、ダランベールの収束判定法によって確認することができる。従ってこれらの級数は、変数 x を複素数全体に拡張することができ、広義一様収束する。つまりこれらの級数によって表される関数は整関数である。解析接続すると、一致の定理より、複素数全体での正則関数としての拡張は一意であり、この収束冪級数で表される。

ここで、 e^x の x を ix に置き換え、e^ix の冪級数が絶対収束することより級数の項の順序は任意に交換可能であることを考慮すれば

{\begin{aligned}e^{ix}&=\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {i^{n}}{n!}}x^{n}\\&=\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {i^{2n}}{(2n)!}}x^{2n} \sum \limits _{n=0}^{\infty }{\dfrac {i^{2n 1}}{(2n 1)!}}x^{2n 1}\\&=\textstyle \sum \limits _{n=0}^{\infty }{\dfrac {(-1)^{n}}{(2n)!}}x^{2n} i\sum \limits _{n=0}^{\infty }{\dfrac {(-1)^{n}}{(2n 1)!}}x^{2n 1}\\&=\cos x i\sin x\end{aligned}}

が得られる。

この公式は、歴史的には全く起源の異なる指数関数と三角関数が、複素数の世界では密接に結びついていることを表している。例えば、三角関数の加法定理は、指数法則 e^ae^b = e^{a b}に対応していることが分かる。

オイラーの公式により、三角関数を複素指数関数で表すことができる。余弦関数、正弦関数は

{\begin{aligned}\cos z&={\frac {e^{iz} e^{-iz}}{2}},\\\sin z&={\frac {e^{iz}-e^{-iz}}{2i}}\end{aligned}}

となる。

証明

この公式には、上記の冪級数展開による証明の他にも異なる幾通りかの証明が知られている。ここにいくつかの例を挙げる。ただし、以下の微分を用いた証明については、実変数を複素数変数におき換えても、これらの議論が成立していることを、別途で証明する必要がある（複素関数論）。

微分による証明

微分方程式による証明

2階線型微分方程式による証明

ロンスキー行列による証明

ド・モアブルの定理による証明

脚注

参照

注釈

参考文献

小笠英志『相対性理論の式を導いてみよう、そして、人に話そう』ベレ出版、2011年1月20日、165-171頁。ISBN 978-486064-267-9。
杉浦光夫『解析入門I』東京大学出版会〈基礎数学2〉、1980年3月31日。ISBN 978-4-13-062005-5。
田村二郎『解析関数』（新版）裳華房〈数学選書3〉、1983年11月15日。ISBN 978-4-7853-1307-4。
Dunham, William (1999), Euler: The Master of Us All, The Mathematical Association of America, ISBN 978-0-88385-328-3, http://paginas.fisica.uson.mx/horacio.munguia/Personal/Documentos/Libros/Euler The_Master of Us.pdf
- W. ダンハム著、黒川信重、若山正人、百々谷哲也訳『オイラー入門』丸善出版〈シュプリンガー数学リーディングス第1巻〉、2019年4月。ISBN 978-4-621-06568-6。 - 注記：2004年6月にシュプリンガー・ジャパンより出版された同名書籍の再出版。
ファインマン、リチャード、レイトン、サンズ著、坪井忠二訳『力学』 I、岩波書店〈ファインマン物理学〉、1977年、294,307頁。ISBN 978-4-00-007711-8。OCLC 47339138。
藤田宏『応用数学』放送大学教育振興会〈放送大学教材〉、1999年3月。ISBN 978-4-595-56042-2。
吉田武『オイラーの贈物　人類の至宝 e^iπ = −1 を学ぶ』（新装版）東海教育研究所、2021年1月。ISBN 978-4-924523-14-2。''e^iπ'' = −1 を学ぶ&rft.aulast=吉田武&rft.au=吉田武&rft.date=2021-01&rft.edition=新装版&rft.pub=東海教育研究所&rft.isbn=978-4-924523-14-2&rfr_id=info:sid/ja.wikipedia.org:オイラーの公式">
- 吉田武『オイラーの贈物　人類の至宝 e^iπ = −1 を学ぶ』筑摩書房〈ちくま学芸文庫〉、2001年11月。ISBN 978-4-480-08675-4。''e^iπ'' = −1 を学ぶ&rft.aulast=吉田武&rft.au=吉田武&rft.date=2001-11&rft.series=ちくま学芸文庫&rft.pub=筑摩書房&rft.isbn=978-4-480-08675-4&rfr_id=info:sid/ja.wikipedia.org:オイラーの公式">