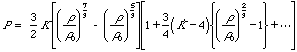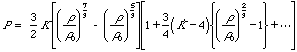バーチ・マーナハンの状態方程式

バーチ・マーナハンの状態方程式（バーチ・マーナハンのじょうたいほうていしき、英: Birch–Murnaghan equation of state）は、1947年にハーバード大学のフランシス・バーチが発表した状態方程式である。等温過程における固体物質の受ける圧力と体積との間の関係を表わす。1944年にジョンズホプキンス大学のフランシス・ドミニク・マーナハンが発表した方程式に基づいており、2人の名前を冠している。

表式

3次のバーチ・マーナハンの状態方程式は次のように書ける。

${\displaystyle P(V)={\frac {3B_{0}}{2}}\left[\left({\frac {V_{0}}{V}}\right)^{\frac {7}{3}}-\left({\frac {V_{0}}{V}}\right)^{\frac {5}{3}}\right]\left\{1 {\frac {3}{4}}\left(B_{0}^{\prime }-4\right)\left[\left({\frac {V_{0}}{V}}\right)^{\frac {2}{3}}-1\right]\right\}}$

ここで、Pは圧力、V₀は参照体積、Vは変形体積、B₀は体積弾性率、B₀′は体積弾性率の圧力に対する微分である_。体積弾性率とその微分は次のように定義される量であり、通常は実験データから回帰により算出される。

${\displaystyle {\begin{aligned}B_{0}&=-V\left({\frac {\partial P}{\partial V}}\right)_{P=0}\\B_{0}'&=\left({\frac {\partial B}{\partial P}}\right)_{P=0}\end{aligned}}}$

この式は、次式で表わされる自由エネルギーfを級数展開することにより得られる。

${\displaystyle f={\frac {1}{2}}\left[\left({\frac {V}{V_{0}}}\right)^{-{\frac {2}{3}}}-1\right]}$

内部エネルギーE(V)は、圧力を積分することにより求められる。

${\displaystyle E(V)=E_{0} {\frac {9V_{0}B_{0}}{16}}\left\{\left[\left({\frac {V_{0}}{V}}\right)^{\frac {2}{3}}-1\right]^{3}B_{0}^{\prime } \left[\left({\frac {V_{0}}{V}}\right)^{\frac {2}{3}}-1\right]^{2}\left[6-4\left({\frac {V_{0}}{V}}\right)^{\frac {2}{3}}\right]\right\}.}$

関連項目

• フランシス・バーチ
• フランシス・ドミニク・マーナハン
• マーナハンの状態方程式
• ローズ・ヴィネットの状態方程式
• アントン・シュミットの状態方程式

参考文献