最小頂点被覆問題

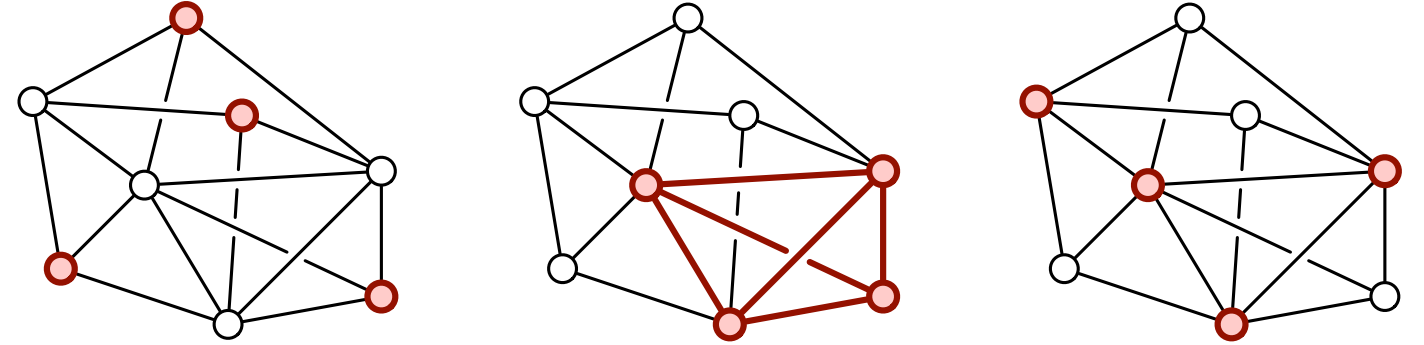
最小頂点被覆問題（さいしょうちょうてんひふくもんだい）は、計算複雑性理論におけるNP困難な問題の一つ。

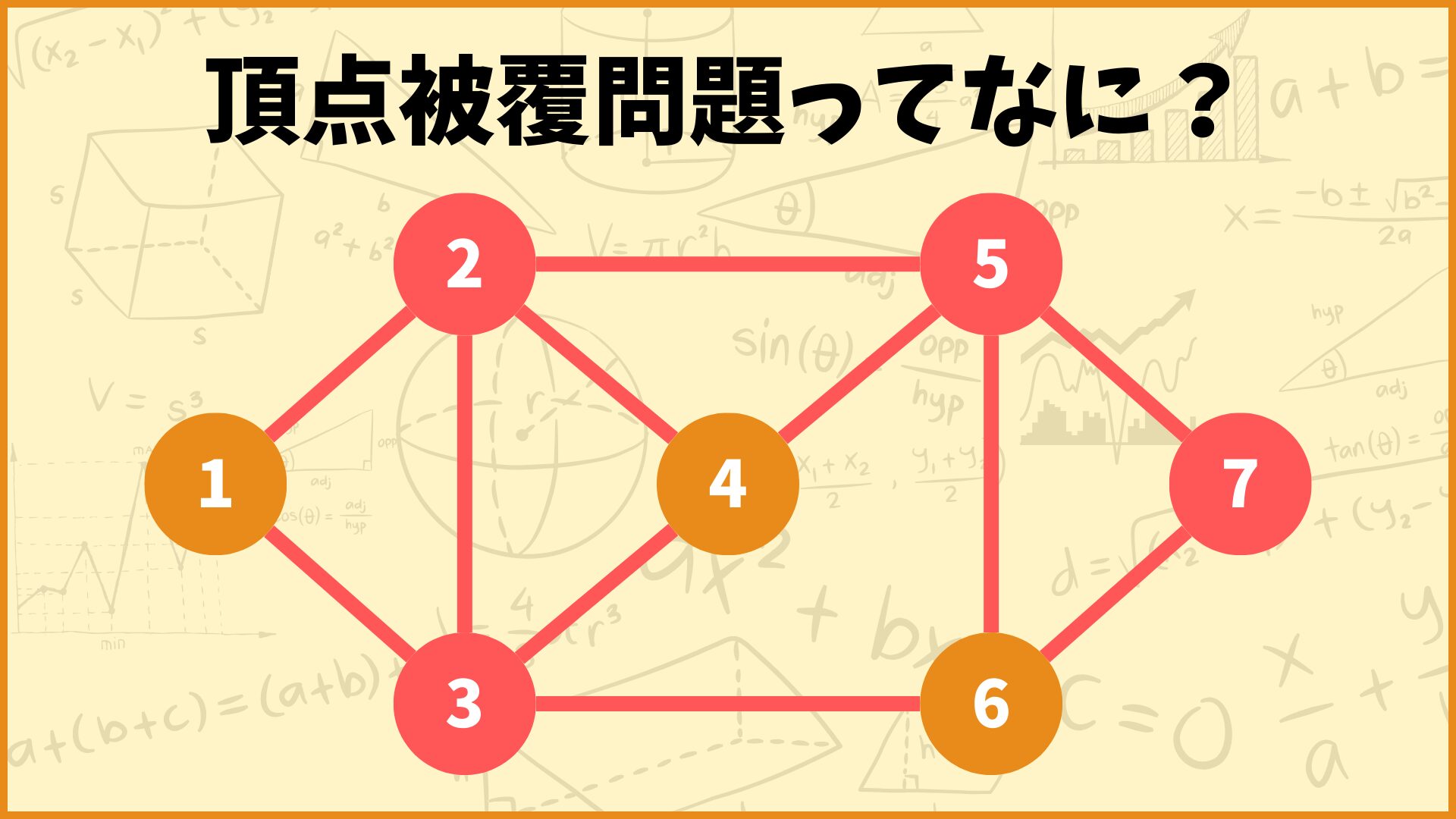
問題: グラフ G(V, E) の各枝 e について端点のいずれか少なくとも一方が、V′ に含まれるような V の部分集合 V′ のうち、|V′| が最小になるものを求めよ

この問題の最適解を求めるのは、NP困難なため、決定性の多項式時間アルゴリズムは存在しないと考えられている。近似アルゴリズムに関して言えば、近似度2の貪欲アルゴリズムが存在することが知られているが、任意の ε > 0 について、近似度 2 - ε の近似度を達成するアルゴリズムも存在しないだろうと考えられている。2005年現在の最良の近似度の下限は、${\displaystyle 10{\sqrt {5}}-21(>1.36)}$ である。

関連項目

• 頂点被覆
• 最適化問題
• 完全被覆問題
• 最大独立集合問題

外部リンク

• MINIMUM VERTEX COVER