2電子原子

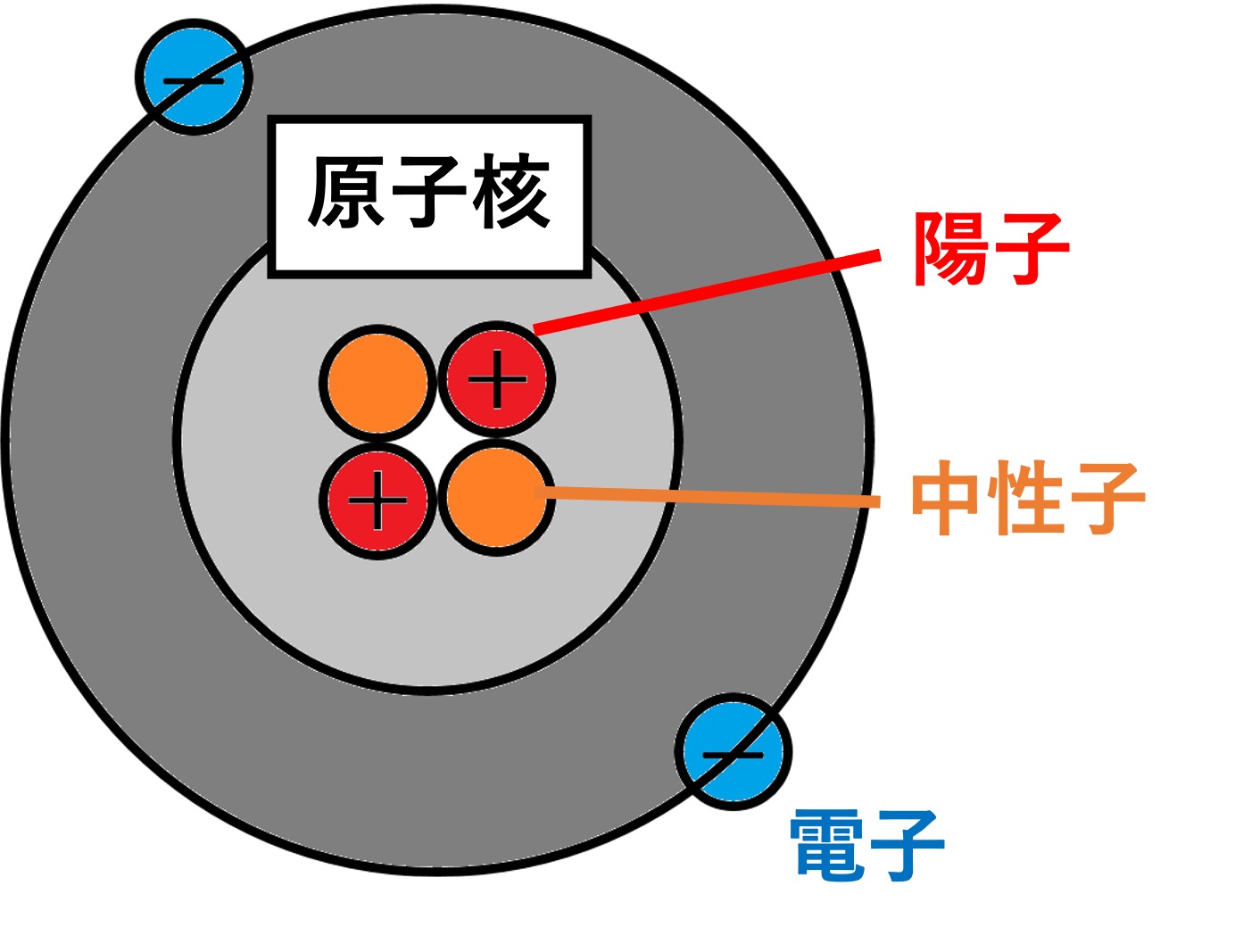
原子物理学において、2電子原子(Two-electron atom)またはヘリウム様イオン(Helium-like ion)は、

Zeの電荷を持つ1つの原子核と2つの電子を持つ量子力学系である。パウリの排他原理が中心的な役割を果たす多電子システムの最初のケースである。また、三体問題の1つの例である。

最初のいくつかの2電子原子の例は、以下のようなものがある。

シュレディンガー方程式

中性のヘリウム原子(He, Z = 2)、陰性の水素陰イオン(H^-, Z = 1)、陽性のリチウムイオン(Li , Z = 3)では、以下のようになるより詳細なシュレディンガー方程式の導出はこちらを参照。

${\displaystyle E\psi =-\hbar ^{2}\left[{\frac {1}{2\mu }}\left(\nabla _{1}^{2} \nabla _{2}^{2}\right) {\frac {1}{M}}\nabla _{1}\cdot \nabla _{2}\right]\psi {\frac {e^{2}}{4\pi \epsilon _{0}}}\left[{\frac {1}{r_{12}}}-Z\left({\frac {1}{r_{1}}} {\frac {1}{r_{2}}}\right)\right]\psi }$

ここで、r₁は1つの電子の位置(r₁ = |r₁|はその大きさ）、r₂はもう1つの電子の位置(r₂ = |r₂|はその大きさ）であり、r₁₂ = |r₁₂|は、以下で与えられる、これらの間の距離の大きさである。

${\displaystyle |\mathbf {r} _{12}|=|\mathbf {r} _{2}-\mathbf {r} _{1}|\,\!}$

μは、質量Mの原子核に対する電子の2体換算質量である。

${\displaystyle \mu ={\frac {m_{e}M}{m_{e} M}}\,\!}$

また、Zは、元素の原子番号である（量子数ではない）。

2つのラプラス作用素の交差項

${\displaystyle {\frac {1}{M}}\nabla _{1}\cdot \nabla _{2}\,\!}$

は、mass polarization termとして知られ、原子核の動きが原因で生じる。

波動関数は、2つの電子の位置の関数である。

${\displaystyle \psi =\psi (\mathbf {r} _{1},\mathbf {r} _{2})}$

この方程式には、解析解はない。

スペクトル

2電子原子の光学スペクトルは、パラの一重線とオルトの三重線の2系列のスペクトル線を持つ。一重線の原子のエネルギー準位は、¹S₀ ¹P₁ ¹D₂ ¹F₃等で示され、三重線では、いくつかのエネルギー準位は分裂している。³S₁ ³P₂ ³P₁ ³P₀ ³D₃ ³D₂ ³D₁ ³F₄ ³F₃ ³F₂。アルカリ土類金属と水銀は、2つの外殻価電子を持つため、似たような特徴を持つ。

関連項目

• 水素原子におけるシュレーディンガー方程式の解
• 水素分子イオン
• ヘリウム原子
• リチウム原子

出典